Research Topics Research Group of Kristina Giesel
Research in the Group of Kristina Giesel
The group’s research includes topics on the dynamics of loop quantum gravity, encoded in the Quantum Einstein Equations, with applications in the context of quantum cosmology and quantum gravitational collapse, as well as open quantum systems that include gravity. We investigate fundamental questions such as the role of physical (quantum) frames in quantum gravity, formulate models and study their physical implications. You can find more detailed information on the individual research topics here.
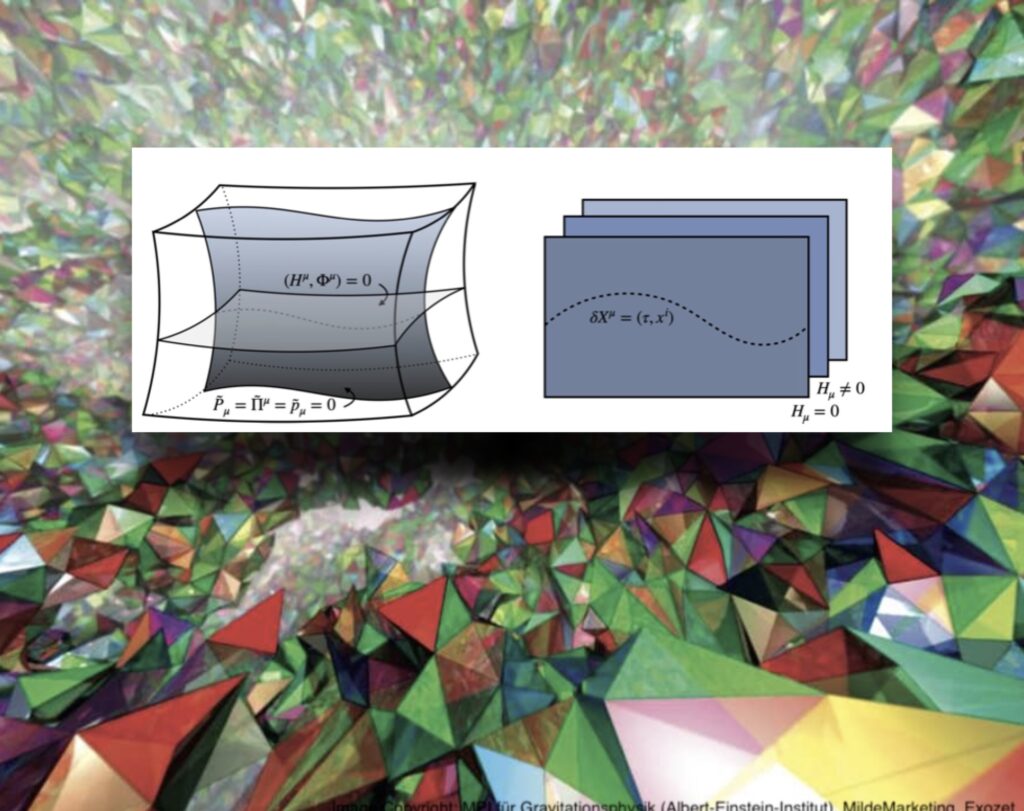
Relational Formalism in the dynamics of (Quantum) Gravity
Physical (Quantum) Reference Frames in the Quantum Einstein Equations and Systems with Gravity
In the canonical approach to loop quantum gravity (LQG), the classical Einstein equations are taken as the starting point. In the classical theory, a specific set of variables is used, known as the Ashtekar-Barbero variables. These allow the Einstein equation to be formulated in the language of a gauge theory, which is also used for the other interactions in quantum field theory in the standard model of particle physics. Since the metric, which describes the geometry of spacetime, is already a dynamical quantity in the classical theory, the aim is to achieve a background-independent quantisation in which the metric also becomes a quantum object. This is in contrast to the standard model of particle physics, in which a fixed classical geometry is chosen and then matter is quantised in this geometry. Therefore, canonical quantisation of general relativity in the LQG framework leads to a non-standard quantum field theory in which the Quantum Einstein Equations can be formulated. The gauge symmetry present in general relativity is associated with the invariance of the theory under generic coordinate transformations, which are called diffeomorphisms. Consequently, the idea of physical, temporal and spatial coordinates, i.e. clocks and rods, with respect to which other quantities evolve, is more complicated than in non- or special-relativistic theories. One way in which clocks and rods can be introduced in general relativiy is through physical dynamical reference frames. These can be understood as observers that are dynamically coupled to gravity, and these can be matter fields, geometric fields or a mixture of both. The dynamics of all fields except the dynamical reference frames is then described in relation to the dynamical reference frames, which can be done in a gauge-invariant way. The group’s research investigates the properties of physical reference frames in the context of the Quantum Einstein Equations, as well as for models in linearised gravity and cosmology, and in open quantum systems.
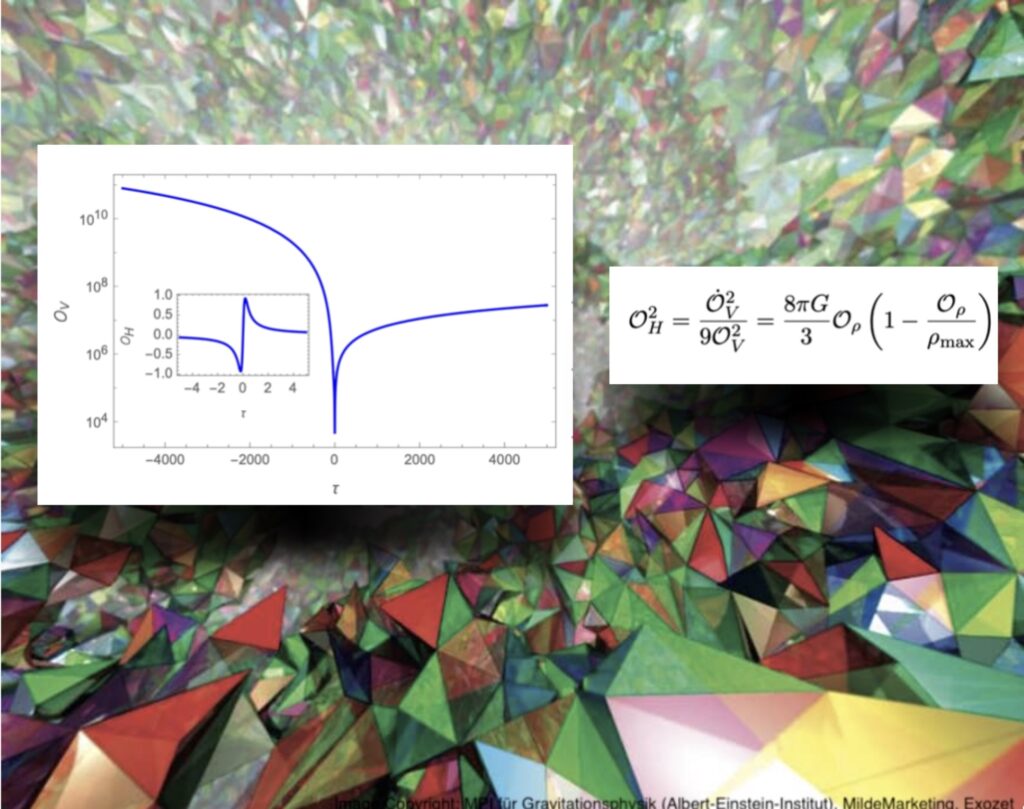
Quantum Einstein Equations: Applications in Cosmology
Quantum Cosmology
Since the Einstein equations in full loop quantum gravity (LQG) are technically very challenging, one approach that researchers in LQG follow is to consider symmetry-reduced models. In these models, the metric is assumed to have certain symmetries, which simplifies the Einstein equations in the classical theory. This has often been a strategy in classical general relativity to obtain exact solutions of the Einstein equations. A prominent example is cosmology, where in the simplest models homogeneity and isotropy reduce the freedom of the metric to one time-dependent scaling factor, whose dynamics and interaction with the matter in the universe is described by the Friedmann equations. The idea of loop quantum cosmology (LQC) is to take the classical cosmological sector as a starting point and then to apply a LQG-inspired quantisation to this sector. The resulting Quantum Einstein Equations in LQC are drastically simplified compared to the full LQG equations and can even be solved analytically in the simplest models. One of the exceptions quantum gravity is that it is able to resolve classical singularities, examples of which are the big bang singularity in cosmology or the singularity at the centre of black holes, where quantities in the Einstein’s equations become infinite and the theory looses its predictive power. A common feature of the models in LQC is that they do not contain any central singularities, so in a simple cosmological FLRW model the big bang singularity is replaced by a big bounce. Evolving such a universe backwards from today, one obtains a contracting universe that never reaches a singularity in the past, but shrinks to a minimal volume and then expands again. For the dynamics captured by the quantum Einstein equations in LQC, effective techniques have been derived that are modified classical equations that encode quantum corrections and closely mimic the behavior of the dynamics obtained by numerically solving the Quantum Einstein equations in LQC. These effective dynamics have also been extended to incorporate more full LQG input, which is very interesting since symmetry reduction and quantisation do not commute. Therefore, one might expect that a first quantisation and subsequent implementation of symmetry reduction could yield some additional insights, although this is technically more demanding than the other way around. The research group studies specific models in LQC, with a focus on different dynamical reference frames. Another research topic is the theory of cosmological perturbations, which studies perturbations around a given cosmological solution. These perturbations, and their subsequent quantisation, play a major role in the predictions for the power spectrum of the cosmic microwave background, which provides access to the physics of the very early universe. The group has worked on a formalism to carry out cosmological perturbation theory in an manifestly gauge-invariant way, where gauge invariance is ensured not only up to the order in the perturbation theory, but for any order. Currently, the group has started to investigate possible implications of cosmological perturbation theory when assuming an LQC quantum background instead of a classical one, a topic that several other quantum gravity groups worldwide are also working on.
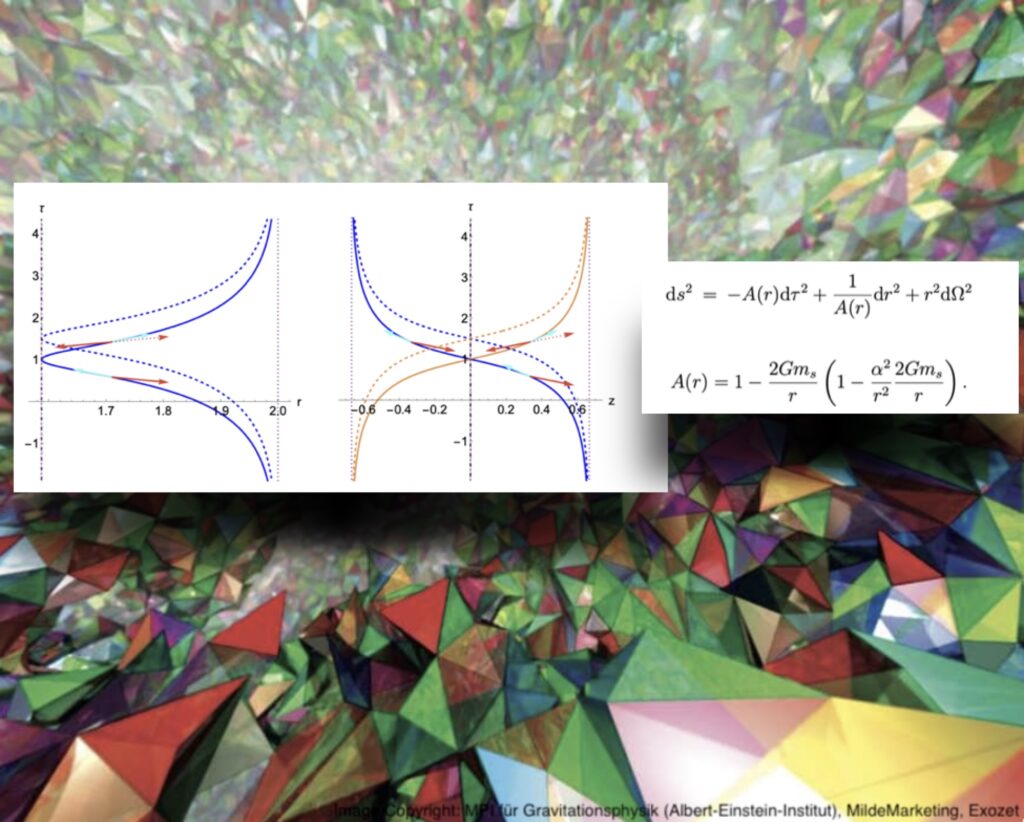
Quantum Einstein Equations: Applications in Spherically Symmetric Models
Quantum Gravitational Collapse and Quantum Black Holes
Another interesting and more complex model with reduced symmetry are models with spherical symmetry. In vacuum, when there is no matter, this corresponds to black hole solutions in the classical theory. When dust is added to the system, there are solutions known as LTB solution. The latter allow the description of the gravitational collapse and a prominent example is the Oppenheimer-Snyder collapse, in which a homogeneous dust sphere is considered to be surrounded by vacuum. As in the cosmological models, the question of whether singularities in these models are resolved when an LQG-inspired quantisation is applied is being addressed in current research in the field of loop quantum gravity. Likewise to loop quantum cosmology, here effective techniques are used to study various models in which the quantum corrections are encoded in specific functions called polymerisation function. The explicit form of these functions can influence the physical properties of these models. For effective models inspired by LQG, these functions are typically sine or cosine functions that encode to some extend the choice of variables and the background-independent quantisation used in LQG. In classical theory, LTB models can be embedded in spherically symmetric models if an additional condition, often referred to as the LTB condition, is applied, and this must be done in accordance with the dynamics. Since the effective dynamics are modified with respect to the classical dynamics, the research group has recently studied the question of whether there are compatible LTB conditions in these effective models, thereby extending the existing results in the literature in some aspects. Furthermore, the formalism developed in this context allows for the unified analysis of a broad class of effective models. Since LTB solutions also include the vacuum solution as a special case, we used this formalism to study regular black hole solutions and their properties. This has been done not only for LQG-inspired models, but also for other well-known regular black hole models such as Bardeen and Hayward. The corresponding polymerisation functions are unbounded functions in the latter case, whereas they are bounded for LQG-inspired models. What all these models have in common is that the central singularity is resolved. If these models are extended to LTB models with inhomogeneous dust profiles, shell-crossing singularities still occur. In this case, weak solutions, also known as shock solutions, must be constructed. The investigation of shock solutions, the question of whether there are effective models in which there are no shell-crossing singularities as well the relation of these models to modified gravity models in the context of extended mimetic gravity are topics that the research group is currently working on.
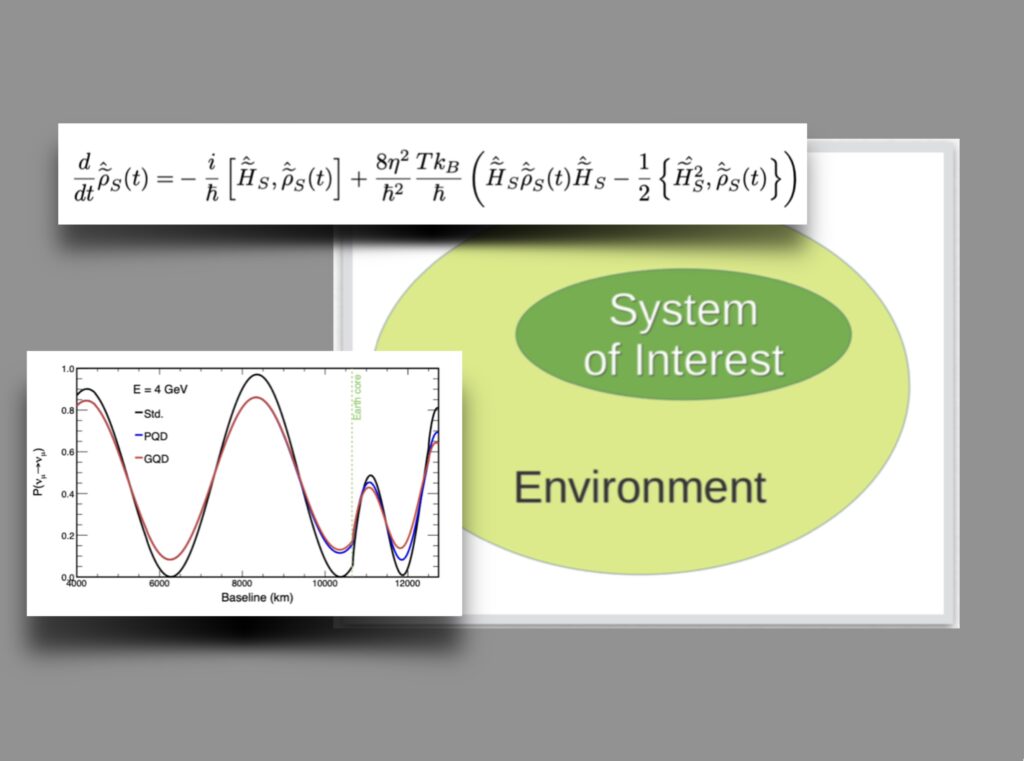
Open Quantum Systems
Gravitational Decoherence and Applications in Astroparticle Physics
In the case of physical models, it is often assumed that the system in question can be completely isolated from its environment and thus treated as an isolated system, which is usually not the case in realistic experiments. If this idealisation is abandoned, the environment and the interaction between the system and the environment must be modelled in addition to the system itself. In the approach to open quantum systems this is done by starting with a total system that included the system, the environment as well as their interaction, usually formulated in terms of a Hamiltonian system. When approaching open quantum systems, one starts with an intial total system that encompasses the system, the environment and their interaction and is usually formulated as a Hamiltonian system. The dynamics of the total system can be described using the von- Neumann equation that encodes the evolution of the total density matrix. Since the total system with all the details of the environment is usually very complicated, the aim is to obtain the effective dynamics of the system of interest, which describes the evolution of the system under the influence of the environment. Technically, such an evolution equation, called master equation, is obtained by tracing out the degrees of freedom of the environment in the von Neumann equation. The master equation includes, in addition to the unitary dynamics that are also present in the closed system when there is no environment, a contribution called the dissipator. The additional dissipator encodes effects like decoherence and dissipation which are induced from the system’s interaction with the environment. A prominent example of such a master equations is the Lindblad equation. The research group particularly investigates open quantum systems that involve gravity. Our most recent work has been on quantum field theory models for open quantum systems in the context of linearised gravity, where matter is coupled to linearised gravity. Matter is chosen as the system of interest and gravity as the environment, leading to models of gravitationally induced decoherence. Since the field-theoretical master equations are technically demanding as a first step, we have investigated the one-particle sector and were particularly interested in how the renormalisation of the master equation can be carried out at the field theory level and to what extent certain approximations such as the Markov and rotating wave approximations, which are often used in non-relativistic quantum mechanical models, can be applied. At the same time, we extended an existing quantum-mechanical toy model for gravitationally induced decoherence to apply it in the context of neutrino oscillations. When treating neutrinos in an open quantum system approach, the probabilities for neutrino oscillations are expected to change. There are several phenomenological models in which the dissipator is parameterised by so-called decoherence parameters. Based on a microscopic model and the derivation of the corresponding master equation, we were able to determine the decoherence parameters and gain new insights into their physical properties. The work on neutrino oscillations was carried out in collaboration with experimentalists from the neutrino group of the Erlangen Centre for Astroparticle Physics (ECAP), to which the Institute for Theoretical Physics III belongs. In addition, Kristina Giesel has been an associate member of the KM3NeT collaboration since June 2024 and Renata Ferrero and Roman Kemper became associate members in November 2024.
More details on recent results in the research group
Here you can find more details on our recent results with links to current publications. Please click the individual links on the pictures (this part is still under construction and will be completed soon, links are not available yet).